
계속해서 이어지는 RSA 관련 암호학 문제
이전 문제보다 훨씬 쉬운 느낌이다.
RSA는 지금까지도 아주 많이 사용하는 공개키 알고리즘의 이름이다.
개발자인 Rivest, Shamir, Adleman 세명의 이름 앞글자를 따서 RSA 라고 이름을 붙혔다.
엄청나게 큰 숫자일수록 소인수분해가 어렵다는것에 착안해서 설계되었다.
RSA의 원리는 아래와 같다.
1. 두 소수 p, q를 준비한다.
2. p-1, q-1과 각각 서로소(1외에는 공약수가 없는 수)인 정수 e를 준비한다.
3. ed를 (p-1)(q-1)으로 나눈 나머지가 1의 되도록 하는 d를 구한다.(d는 개인키로 공개하지 않는다)
4. n=pq를 계산한 후 n과 e를 공개한다.(이 둘이 공개키)
이 알고리즘을 이용해서 공개키-개인키 쌍을 만들고
공개키로 암호화했다면 개인키로만 풀 수 있고, 개인키로 암호화했다면 공개키로만 풀 수 있는 그런 알고리즘이다.
Modulus: 98570307780590287344989641660271563150943084591122129236101184963953890610515286342182643236514124325672053304374355281945455993001454145469449640602102808287018619896494144221889411960418829067000944408910977857246549239617540588105788633268030690222998939690024329717050066864773464183557939988832150357227
One factor of N: 9695477612097814143634685975895486365012211256067236988184151482923787800058653259439240377630508988251817608592320391742708529901158658812320088090921919
Public key: 65537
Ciphertext: 75665489286663825011389014693118717144564492910496517817351278852753259053052732535663285501814281678158913989615919776491777945945627147232073116295758400365665526264438202825171012874266519752207522580833300789271016065464767771248100896706714555420620455039240658817899104768781122292162714745754316687483
문제에서 제공되는 ciphertext.txt 파일의 내용은 위와 같다.
Modulus, One factor of N, Public Key, Ciphertext 가 각각 주어진다.
여기서 Modulus 가 위에서 언급한 N 값인데,
원래 RSA는 이 N값이 워낙 크고,
두 소수를 곱해서 N이 되는 각각의 소수를 찾는게 어렵기 때문에 그만큼 안전한 것인데,
여기선 웃긴게 One factor of N 이라고 해서 두 소수중 하나를 알려주고 있다.
그러니까 N = pq 에서 p 값을 알려준거나 마찬가지이다.
그럼 N/p = q 니까 간단하게 q 값을 구할 수 있게 된다.
그럼 e, p 와 q 값을 알고 있으니
ed 를 (p-1)(q-1) 로 나눈 나머지가 1이 되도록 하는 d 값도 구할수 있게되고,
d는 개인키이니 d를 사용해서 암호문을 해독할 수 있게 된다.
github에 보면 RSA문제를 풀 때 사용하는 RsaCtfTool 이라는 좋은 도구가있다.

git clone [github 주소] 명령어를 통해 다운로드 받을 수 있다.
다운로드 받고나서 cd RsaCtfTool 명령어로 해당 폴더에 들어가보면
RsaCtfTool.py 라는 파이썬 파일이 보이게 된다.

./RsaCtfTool.py 라고 입력하면 실행이 가능한데
이렇게 No module named 'Crytpo' 라는 에러가 나게되면

pip install pycrypto 명령어로 다운로드 받아주면 된다.

다운받으면 이렇게 잘 실행이 된다.
이제 옵션을 줘서 툴을 실행시키면 된다.
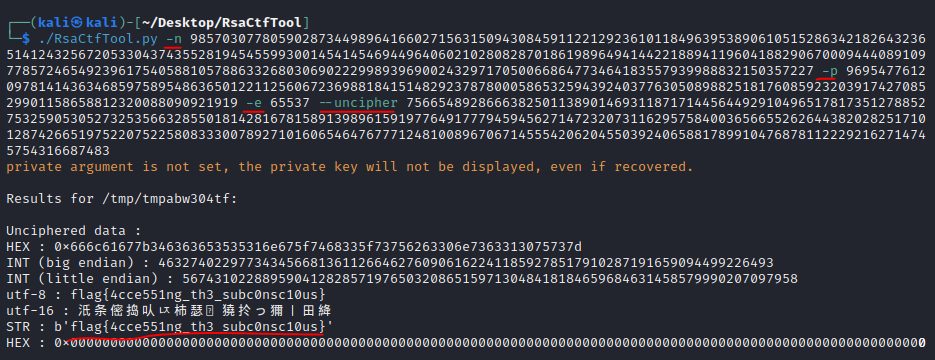
-n 옵션에 Modulus, -p 옵션에 One factor of N, -e 옵션에 Public Key,
--uncipher 옵션에 Ciphertext 에 있는 값을 넣어주게 되면
평문으로 된 플래그를 찾을 수 있다.
'CTF > 암호학' 카테고리의 다른 글
| [Cyber Security Rumble] Hashfun - 암호학 / XOR / Python (60) | 2022.12.21 |
|---|---|
| [TeamH4C CTF] The Easiest problem of the universe - 암호학 / Base64 / Binary (49) | 2022.12.17 |
| [b01lers CTF] Clear the Mind - 암호학 / RSA / Python (36) | 2022.11.26 |
| [2020CCE] Easy RSA - 암호학 / RsaCtfTool / Python (42) | 2022.11.06 |
| [TigerKingCTF] Swag - 암호학 / QR코드 (66) | 2022.07.27 |