
푸는데 머리조금 아팠던 리버싱 문제이다.
역시나 수학은 어려운것 같다..
문제에서 주어지는 것은 be_true 라는 바이너리 파일이다.
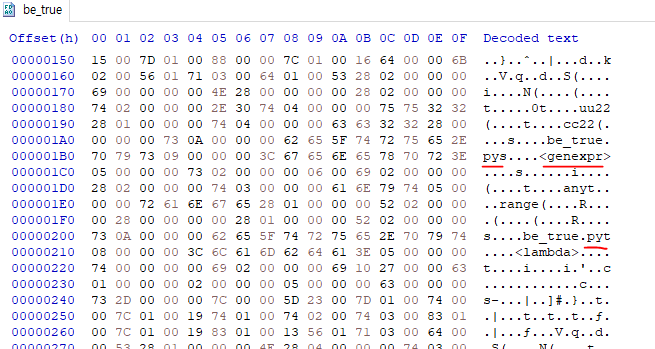
무슨 파일인지 보려고 HxD로 열어봤는데
중간중가네 pys, pyt 이런 단어들이 보여서
파이썬으로 만들어진 것이라고 추측했다.
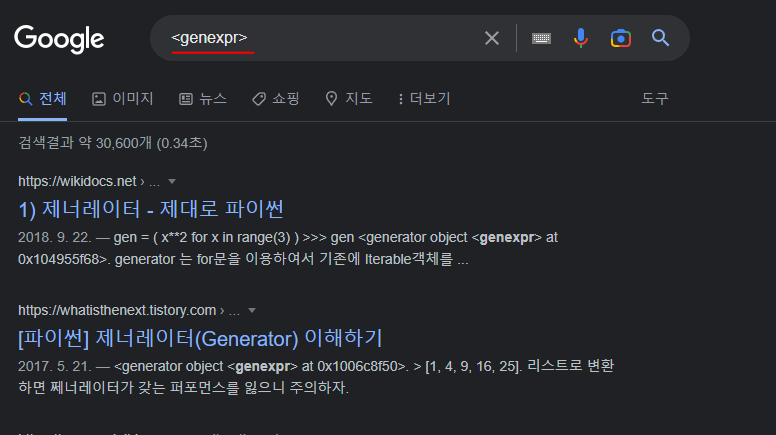
확실하게 파이썬이라고 생각한건
<genexpr> 을 구글에 검색한 결과 파이썬 제너레이터라는 검색결과가 나왔기 때문이다.

그래서 해당 파일의 확장자를 .pyc 로 바꾸고 분석을 시작했다.

.pyc 파일을 파이썬 코드로 복구하는데는 uncompyle6 라는 도구를 사용한다.
pip install uncompyle6 라고 입력하면 다운로드 받을 수 있다.

python3 uncompyle6 <pyc파일> 이라고 입력하면
이렇게 파이썬 코드를 복구할 수 있다.
import operator
flag = 0
power = (12 * flag + 44) / 4 - 1234 / 617 * flag - sum([1, 4, 7])
flag *= power
ppc = filter((lambda cc22: not any(cc22 % uu22 == 0 for uu22 in range(2, cc22))), range(2, 10000))
dat = reduce(operator.mul, (ppc[i] ** int(str(flag)[i]) for i in range(len(str(flag)))))
print dat == 3560267726635400465627540581996487760054035685444946475657505105403063442856963534755133504166293811169018648637812735995934052617540980495952470560844800443626277335201401028364068797946796579956457852457279957300619892623751175557650873016730889125068146398488627192356718363004881175012104986391177956396290571688585499385019181192105543180552708742672275440530116680223358366613050183523086165910780504269235376773473500
이런 코드가 나온다.
flag 변수와 power 변수가 보인다.
power 변수가 굉장히 복잡해 보이는데
power 를 계산하면 결국 flag - 1 이 된다.

실제로 flag 에 어떤 값을 넣은 뒤, flag와 power를 순서대로 출력하면
위와 같은 결과가 나온다.
자료형이 조금 바껴서 그렇지 power는 결국 flag - 1 값을 가진다.
ppc = list(filter((lambda cc22: not any(cc22 % uu22 == 0 for uu22 in range(2, cc22))), range(2, 10000)))
print(ppc)
ppc는 뭔가 싶어서 한번 출력해봤다.
저렇게 앞에 list()를 붙히면 filter 오브젝트를 출력 가능하다.

이게 출력 결과의 일부인데
가만 보니 2부터 10000 사이에 있는 소수들의 집합인듯 했다.
그다음은 뭔가를 계산해서 dat 에 저장하고
dat 에 있는 값이 어떤값인지 비교해서 출력하는 코드이다.
3560267726635400465627540581996487760054035685444946475657505105403063442856963534755133504166293811169018648637812735995934052617540980495952470560844800443626277335201401028364068797946796579956457852457279957300619892623751175557650873016730889125068146398488627192356718363004881175012104986391177956396290571688585499385019181192105543180552708742672275440530116680223358366613050183523086165910780504269235376773473500
주어진 이 값을
역으로 계산해서 뭔래 어떤 값이었는지 알아내면 문제를 풀 수 있다.
import operator
ppc = filter(lambda cc22: not any(cc22 % uu22 == 0 for uu22 in range(2, cc22)), range(2, 10000))
target = 3560267726635400465627540581996487760054035685444946475657505105403063442856963534755133504166293811169018648637812735995934052617540980495952470560844800443626277335201401028364068797946796579956457852457279957300619892623751175557650873016730889125068146398488627192356718363004881175012104986391177956396290571688585499385019181192105543180552708742672275440530116680223358366613050183523086165910780504269235376773473500
flag = ''
for j in range(len(ppc)):
tmp = ['','','','','','','','','','']
b = int(ppc[j])
tmp[0] = target % b
tmp[1] = (target/b) % b
tmp[2] = (target/b/b) % b
tmp[3] = (target/b/b/b) % b
tmp[4] = (target/b/b/b/b) % b
tmp[5] = (target/b/b/b/b/b) % b
tmp[6] = (target/b/b/b/b/b/b) % b
tmp[7] = (target/b/b/b/b/b/b/b) % b
tmp[8] = (target/b/b/b/b/b/b/b/b) % b
tmp[9] = (target/b/b/b/b/b/b/b/b/b) % b
print(b,tmp)
for k in range(0,10):
if tmp[k] != 0:
flag += str(k)
break
print(flag)
코드는 이렇게 작성했다.
ppc는 그대로 가져와서 쓰고
target 변수에 주어진 수를 넣어주었다.
그리고 반복문을 통해 소인수분해 하는것을 구현했다.
대략적으로 설명하면 어떤 숫자를 소인수분해 한 뒤, 지수만 나열해서 쓰는 방식이다.
예를들어 소인수분해한 결과가 (2^3) * (3^4) * (5^5) 이라면
지수인 345 만 써서 flag 변수에 모아 출력시켰다.

코드를 실행시키면 이런 값이 나온다.
뒤에 000... 부분은 의미없는 부분이고
앞에 27 ~ 56 까지가 의미있는 부분이다.
이 값이 flag *= power 의 값이다.
다시쓰면 flag * (flag -1) 의 값이 위의 값이다.
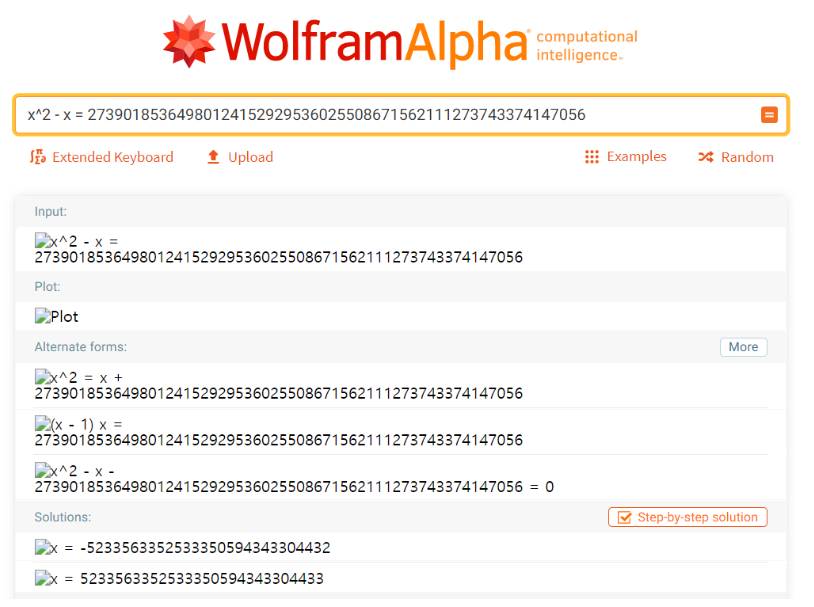
flag 값을 구하려면 방정식의 해를 구해야 한다.
WolframAlpha(https://www.wolframalpha.com/) 라는 사이트에서 쉽게 해를 구할 수 있다.
flag^2 - flag = 27390185364980124152929536025508671562111273743374147056 를 계산하면
flag = 5233563352533350594343304433 이 나오게 된다.

이 값을 CyberChef(https://gchq.github.io/CyberChef/) 에서
From Hex로 디코딩해주면 플래그를 찾을 수 있다.
'CTF > 리버싱' 카테고리의 다른 글
| [LACTF] caterpillar - 리버싱 / 자바스크립트 (66) | 2023.02.23 |
|---|---|
| [justCTF] That's not crypto - 리버싱 / uncomplye6 (58) | 2023.02.15 |
| [JISCTF] Baby Reverse - 리버싱 / IDA (67) | 2023.01.17 |
| [PoseidonCTF] The Large Cherries - 리버싱 / IDA / Pwntool (48) | 2022.11.12 |
| [2020CCE] Easyransom - 리버싱 / IDA / HxD / XOR (42) | 2022.11.04 |